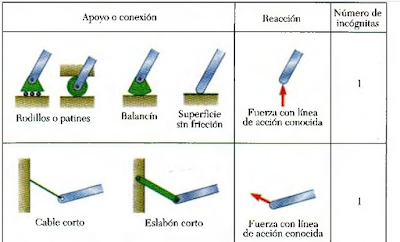
Reacciones en los puntos de apoyo y conexiones de una estructura bidimensional
1.- Determine las componentes del par simple que es equivalente a los dos pares mostrados.
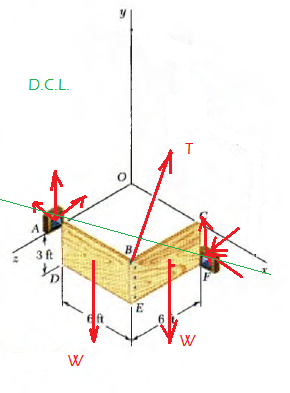
D.C.L.
sum. Fy = 0....
Ay + By- WSen25°=0 ......(1)
sum. Fx= 0
T=WCos25°=5500.cos25°= 4.984,69 lb
sum.MA=0
T.24-25.WSen25°-30-WSen25°+ By.50= 0
By=1760,36 lb....en (1)
Ay=564,04 lb
5.-
6.-
7.-
8.- Reducir el sistema de fuerzas mostradas en la figura, a una fuerza-par en el punto O. Si F1=34 N, F2=25 N, F3=24 N, F4=6 N
9.-
10.-
D.C.L.
11.-
12.-
13..-
14.-
15.-
MÉTODO ALTERNATIVO
4.7 Equilibrio de un cuerpo sujeto a tres fuerzas.

16.-
17.-
D.C.L.
18.-
19.-
20.-
21.-
22.-
23.-
24.-
25.-
26.-Localice el centroide del área plana mostrada.
27.-
28.- Figura P5.3
29.-
30.-
31.-
32.-
33.-
34.-
35.-
36.-
d) halle tambien la intersección con el eje xz.
Desarrollo
-12x +35z = 160 x= -13,33 in z = 4,57 in
37.-
DESARROLLO
38.-
39.-
40.-
41.-
42.-
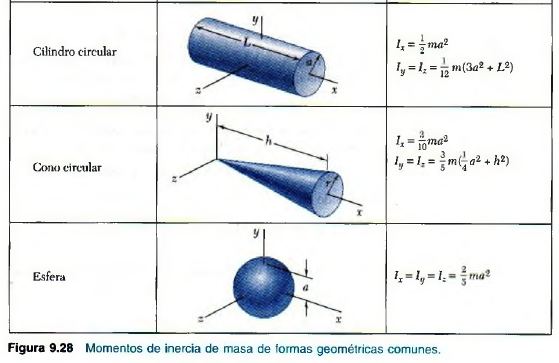
MOMENTO DE INERCIA EN GENERAL
DE UN PUNTO MATERIAL, EN RELACIÓN A UN PLANO, A UN EJE O A UN PUNTO, ES EL PRODUCTO DE LA MASA DEL PUNTO, POR EL CUADRADO DE LA DISTANCIA, AL PLANO , AL EJE O AL PUNTO, RESPECTIVAMENTE.
43.-
44.-
45.-
EN TODOS LOS GRUPOS SE PIDE DETERMINAR LA ECUACIÓN DEL ELIPSOIDE CON RESPECTO AL EJE ARBITRARIO.
y sus orientaciones.
peso especifico=7,8 g/cm3
queda anulado m=2Kg
y sus orientaciones.
con respecto a O.
peso especifico=7,80 g/cm3
queda anulado m=3000 g
Determine el momento de inercia del cilindro con respecto a la línea OA.
peso específico=7,80 g/cm3
queda anulado m=500 g
PARA TODOS LOS GRUPOS del 2do. T.P.: UTILIZANDO EL CIRCULO DE MOHR, DETERMINE LOS MOMENTOS PRINCIPALES DE INERCIA Y LA DIRECCIÓN DE LOS EJES PRINCIPALES DE INERCIA, VERIFIQUE CON EL CALCULO ANALÍTICO. GRAFIQUE LA ELIPSE CENTRAL DE INERCIA POR MEDIO DEL RADIO DE GIRO.
(distancias en cm)